Decomposition models
Decomposition of the Radiation Components |
Glossary - In HelioClim-3 - In HelioClim-1 - Other models - Bibliography - Equations
1. Glossary
|
|
2. In HelioClim-3
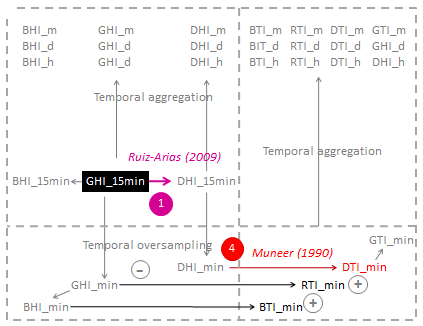
| Starting point: the 15 min Global Horizontal Irradiation data (GHI_15min). Case of HC-3.
The model to compute the diffuse part of the radiation over an inclined surface is Muneer (1990). (Reminder: ESRA (2000): eq. 3.6.5a to eq. 3.6.7b, pp:142-143). Then, a temporal aggregation is performed if requested by the user and the components are summed up to formed the Global fraction. NB: since Apr. 2013, the algorithm of Muneer computes the DTI with or without horizon. |
3. In HelioClim-1
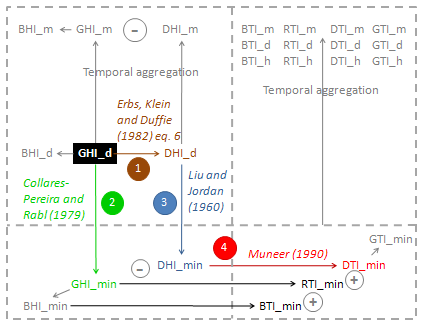
| Starting point: the daily Global Irradiation data over the horizontal plane (GHI_d). Case of HC-1.
|
DHI_min: the algorithm of Liu and Jordan (1960), described in the ESRA (2000), permits to assess the hourly (or on smaller time intervals) diffuse fraction from the global irradiance. ESRA 2000: eq 3.5.25 and eq 3.5.26 p129
DTI_min: The algorithm of Muneer (1990) is exploited to extract the proportion of diffuse radiation collected by any inclined surface. At the origin, this model has been defined on a hourly basis. Nevertheless, it can be extended to an interval of time lower than the hour since it uses Kc. ESRA (2000): eq. 3.6.5a to eq. 3.6.7b, pp:142-143
BTI_min: the direct (Beam) component computation over the inclined surface is based on pure geometry, directly obtained from the BHI
RTI_min: the reflected component is a fonction of the GHI_min, the albedo and of the tilt of the plane (similar to the proportion of sky seen by the tilted surface): RTI_min = GHI_min*albedo*(1-cos(tilt))/2
Then, temporal aggregation is performed if requested by the user and the components are summed up to formed the Global fraction.
NB: since Apr. 2013, the algorithm of Muneer can compute the DTI with or without horizon.
4. Other models
Several other models exists to compute DTI from DHI. Among them, the most popular is Perez et al. 1987. This approach is similar to the one of Muneer 1990, since it exploits an anisotrope representation of the sky vault decomposing the sky in 3 zones: the diffuse "horizon", the diffuse "circumsolar" and the diffuse "isotrope" to represent the rest of the sky. The only difference resides in the use of different empirical functions, i.e. the parameters to describe the models have been estimated using different cases. There is no scientific or physical demonstration that would prefer one method from the other one.
The model described in Perez et al. 1987 is a simplification of the model of radiance of Perez et al. 1993, which proposes an analogical distribution of the sky. This approach is classic for daylighting applications, but not really for radiation. Moreover, as the numerical implementation of this model implies to decompose the sky into a very high number of very small elements, the code is very long to run and return a result, which is not suitable for an operational exploitation.
5. Bibliography
Main publications are: Erbs 1980, Erbs, Klein and Duffie, 1982, ESRA 2000, Muneer 1990, Perez and Seals 1987, and Perez et al. 1993.
Full references are available on the "publication" page.
6. Equations
 |
Erbs, Klein and Duffie (1982), eq 6. |
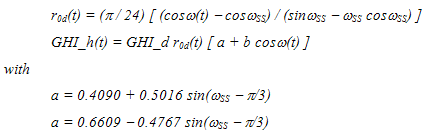 |  Collares-Peirera and Rabl (1979) |
 |
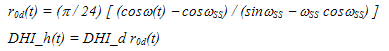Liu and Jordan (1960) |
 | Muneer (1990) |